Other features:

 enter
'3+3' EXE ->
enter
'3+3' EXE ->
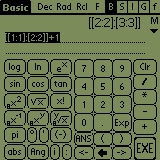
Now to some of the things you can see on screen. The 'Rcl' is for fast access to variables, 'F' is for fast access to functions (be sure and create your own - see below) and 'H' stands for history.
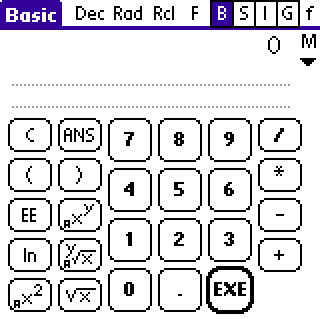
There are 2 different layouts of the Basic screen. You can switch it
in Preferences. The second form of the Basic layout is more crowded, but
some people like it.
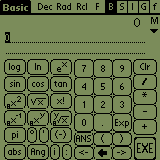
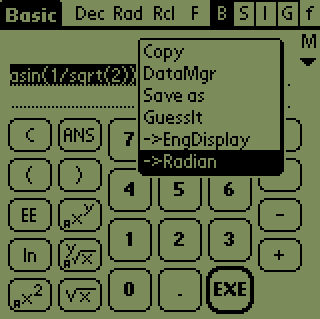


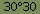 . But only, of
course, if you learn how to write the special degree character, or select
the Basic=>Scien check box in Preferences to get a Basic screen that has
the degree and minute characters (right hand figure above). The Degree/Radian/Grad
can be switched in Preferences or as a convenience you can change the mode
by tapping the Deg/Rad/Grd indicator at the top of the display. Selection
of Dec/Hex/Oct/Bin can be made in the same way. This saves time in
that you do not need to go to Preferences Screen to change trig modes or
number radix.
. But only, of
course, if you learn how to write the special degree character, or select
the Basic=>Scien check box in Preferences to get a Basic screen that has
the degree and minute characters (right hand figure above). The Degree/Radian/Grad
can be switched in Preferences or as a convenience you can change the mode
by tapping the Deg/Rad/Grd indicator at the top of the display. Selection
of Dec/Hex/Oct/Bin can be made in the same way. This saves time in
that you do not need to go to Preferences Screen to change trig modes or
number radix.
NOTE: You must be in Deg mode vs. Rad or Grd to enter numbers in degrees!
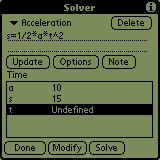
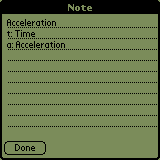
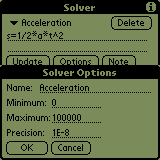
You can use the solver to store and document your formulas. If there
is no '=' found, Solver just computes the result.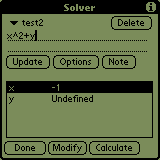
f()="function expression"EasyCalc offers the ability to define functions so that you can use them later.
f()="x^2-4"
f(5)

 You get the answer 21.
You get the answer 21.
fzero(min:max:func[:error[:params]])This function finds the root of a function using the method 'division of interval'.
Example:
fzero(-1:4:"x^3-x^2-5")

f()="x^2-4"
fzero(-1:4:f())

It is possible to add additional parameters to the function being solved. All parameters that are passed to fzero() after the error parameter are passed to the inner function.
fzero(-100:100:"x(2)*x^2+x(3)*x+x(4)":1E-8:2:3:-2)This function would solve a quadratic function a*x^2+b*x+c, where a is 2, b is 3 and c is -2.
fvalue(min:max:value:func[:error[:params]])The function fvalue tries to find a point where f(x)=value.
fintersect(min:max:f1:f2[:error[:params]])
The function fintersect tries to find a point where f1(x)=f2(x).
All restrictions of function fvalue apply to these 2 functions.
Example:
fromberg(-1:4:"x^3+x^2-5")
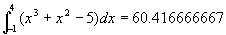

fd_dx(x:func[:error[:params]])EasyCalc supports finding the first and second derivatives of a function. The function fd_dx finds the first derivative at the point x and the function fd2_dx finds the second derivative at the point x.
fd2_dx(x:func[:error[:params]])
Example: Let's have the function 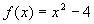 where
the derivative is
where
the derivative is 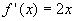 . Let x=2, then
. Let x=2, then 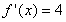 .
.
fd_dx(2:"x^2-4")

[[:a11:a12:...]:[a21:a22]:...[...: anm]]This form creates a user defined matrix.

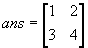
Example: b=[[1.1:1.2]:[1.3:1.4]:[1.5:1.6]]


b=[[1:i]:[i:3]]

(matrix_a)+(matrix_b)Easycalc supports all standard matrix operations like adding, subtracting and multiplying matrices.
(matrix_a)-(matrix_b)
(matrix_a)*(matrix_b)




identity(n)This function generates an identity matix with dimension n.


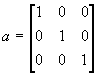
(matrix_a)^(-1)Example:
(matrix_a)'
a=[[1:2]:[3:4]] a^(-1)




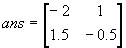
Example:
a=[[1:2:3]:[4:5:6]]
b=a'



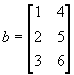
rref(a)This functions reduces dependent rows, it is usually used to find a solution to system of equations.
1x + 2y = 3
4x + 5y = 6Put these two linear equations in matrix form with right hand side appended as right column.
a=[[1:2:3]:[4:5:6]]
rref(a)A row echelon form is returned as evidenced by the leading 1's propagating downward and to the right.
The results for x and y are returned as the right column of rref(a). And the solution can be
verified, see below.1*(-1) + 2*(2) = 3
4*(-1) + 5*(2) = 6



qrq(a) and qrr(a) return Q and R respectively as Factorization of matrix aThe qrq and qrs functions combined will compute the orthogonal Q, and upper triangular R matrix, respectively, of an m x n matrix using Householder method. For m = n, Q and R are the same size as the original matrix. For m(rows) x n(cols) the Q matrix is size m x m and R is size m x n. The result of qrq(a) * qrr(a) should return the original matrix ' a '. QR generally decomposes a full rank matrix to a simpler form.qrs(Ab) solves linear equation Ax = b like rref only using QR decomposition and backsubstitution. This approach may
solve matrix that are not solvable with rref.
Examples:
First enter a matrix --- ' mat3_4=[[1:2:3:4]:[2:3:4:5]:[3:4:5:6]] '
then try --- ' qrq(mat3_4) '
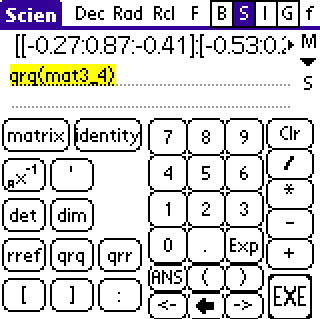
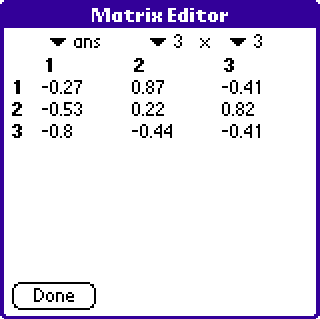 Q
Q
and ' qrr(mat3_4) '
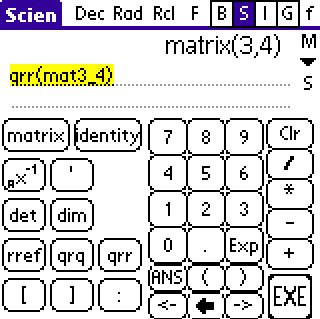
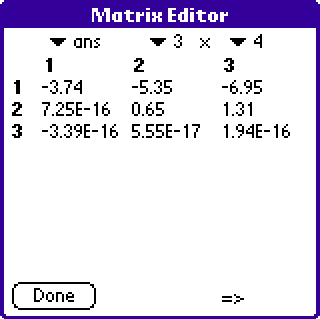 R - upper triangular - but zero is near 1e-16.
R - upper triangular - but zero is near 1e-16.finally try ' qrq(mat3_4) * qrr(mat3_4) '
 The original matrix - use => to see remaining columns.
The original matrix - use => to see remaining columns.Given Q and R, problems such as Ax = b can readily be solved
by replacing A with QR. This is readily accomplished with function
qrs.
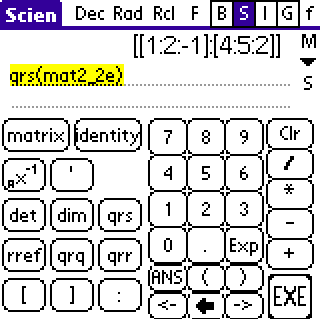
In this example the same matrix a appended with b as used above for
rref was entered into mat2_2e. The original a is returned along with
the solution x which is -1, 2. Note: The Matrix can be complex
but also note that for qrs the matrix must currently be square.


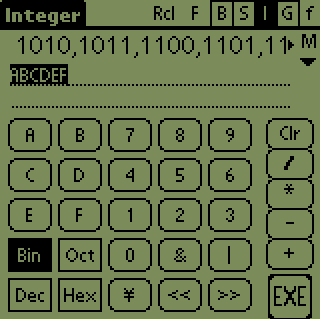 In this example enter 'ABCDEF' with HEX selected then select BIN.
In this example enter 'ABCDEF' with HEX selected then select BIN.


You can define your own functions that accept more then 1 parameter. You have to call the second parameter as x(2) third as x(3) etc. E.g. f()="x(1)+x(2)".
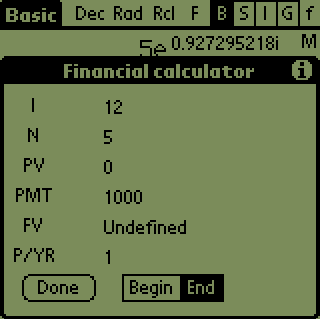
This is a basic implementation of financial calculator. You work with
6 different variables:
IT - interest pr. year. Note: from the 1.01 version this should
be a per-cent number, e.g. 12% interest should be written as i=12
and not as
i=0.12, like in earlier versions.
NP - number of payment-periods
PV - present value
PMT - payment (annuity) every period
FV - future value
P/YR - payments per year
and the Begin/End buttons, that affect when is the payment done - in
the beginning of the year or at the end (usually at the end).
Now you can try defining 5 variables and by tapping on the name of
the 6th it gets computed. Let's try an example:
By tapping on the buttons 'Undefined' near names of corresponding variables
you can enter values for every variable. Now most of those 'Undefined'
messages should have disappeared. If you tap on the name of the variable
you wanted to compute, a notice 'Please wait' will appear in the middle
of the screen indicating, that the calculator is computing, and you'll
be able to read the result as soon as the sign disappears.
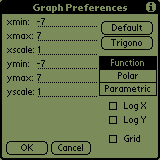
Let's begin with drawing a simple graph. Go to graph preferences (tap
'G' and then the letter 'P' or 'menu->Graph->preferences') and set it exactly
as you can see it on the screen-shot.
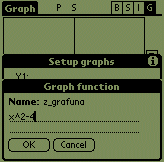
Now exit the preferences and go to setup (tap 'S' or 'menu->Graph->Setup
funcs'). Tap the blank space on the right of 'Y1' and enter "x^2-4". Exit
setup and look at the graph. If you see the graph to be drawing too fast,
you can make it faster by tapping the 'Sp' button and choosing the speed.
For the higher speed you get lower quality though.
If you want to delete a function or graph an already existing one,
tap on the function identifier (Y1,r1...) and a popup menu appears. Select
'None' to hide a function, 'User' to create a special function for this
graph (the same one, as when you tap to the right of the identifier) or
choose an already existing function.
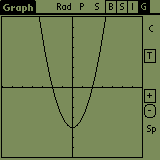
What can you do with the graph screen? If you tap on the graph and
move the pen, the graph moves too. After you lift the pen, the graph is
redrawn. The '-' button is for 'zoom out' and the '+' button is for 'zoom
in' (press the '+' button and draw a rectangle, where do you want the new
screen to be).
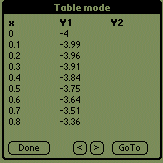
If you want to read the graph values, go to Menu->graph->table mode, and what you read are values of the parameter (x) and values of f(x).
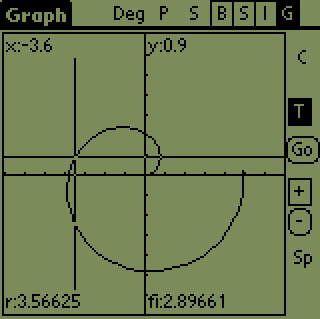
You may want to trace a function like in the older version of EasyCalc.
Tap the 'T' on the right, select a function and tap on the screen. This
works perfectly for normal functions, but works somewhat worse for Polar
and doesn't work at all for Parametric functions. That's why you can use
up/down arrows and/or the 'Go' button to draw a cross directly on some
value. You may also start typing the value directly by graffiti and the
'GoTo' window appears automatically.
 Parametric
'Art' ?
Parametric
'Art' ?
EasyCalc can do some numerical mathematics, it can compute root, minimum
and maximum of a function, first and second derivation and integral. Tap
the 'C' button on on the right side of screen and follow instructions.
Result of the computation will be stored in a variable called 'graphres'.
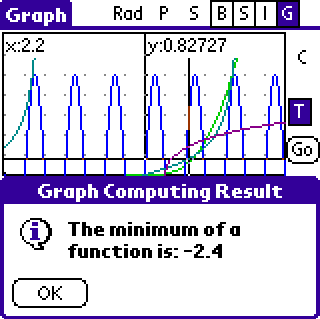 Selected 'C' and minimum then set left and right boundaries ...
Selected 'C' and minimum then set left and right boundaries ...
Lists can be thought as an extension of computation engine of EasyCalc. Most normal operation accept lists and produce a list as a result. E.g. sin(list(0:pi/2:pi)) = list(0:1:0). Of course you can freely add, subtract, multiply lists. The variation of a list can be easily defined as: sum(x-sum(x)/ldim(x))/ldim(x) (and it will work with complex numbers).
Lists work with these functions:
EasyCalc was written by Ondrej Palkovsky, ondrap@penguin.cz. Latest information is available on http://easycalc.sourceforge.net. I send many thanks to people who reported bugs and sent me language corrections to this tutorial. This product is still changing and if you feel that you encountered a bug (including an error in this tutorial, english is not my first tongue) feel free to contact me.