3.1 古典論力学における軌道

　軌道というものを簡単にイメージするために、まず地球とその周りを回転している月の運動を考えてみましょう。このとき地球と月の引力は

となり、角運動量について注目すると以下の示すように角運動量保存則が成立しています。

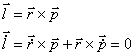
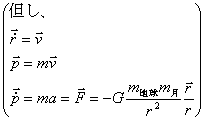
よって角運動量は時間によらず一定であり、任意の時間で常に角運動量は同じ向き・大きさを持っていることがわかります。また、この回転運動は平面的に行われており、角運動量が軌道を決定していることが分かります。

3.2 量子論的な軌道

　元素の核の周りには電子が回転しているが、この電子はどのような軌道を描いているのでしょうか？簡単な例として水素原子のシュレディンガー方程式を考えてみます。この描像は、地球の周りをまわる月の運動を量子論的に考えたものと言い換えることが出来ます。

ここで、とおく。は球面調和関数を示しており、この関数が軌道の形状を決定します。また以下の関係が成立します。

nは軌道のエネルギー決定しています。各元素における軌道のエネルギー準位に注目してみると、fig.3.1の示すように、nが大きければそれだけエネルギー準位が高くなっていることが分かります。また、l, mは軌道の形状を決定してる。形状は方位量子数lと磁気量子数mに依存しています。例えば、3d軌道では磁気量子数の違いによってfig.3.2の示すように異なる形状をしています。

3.3 軌道自由度

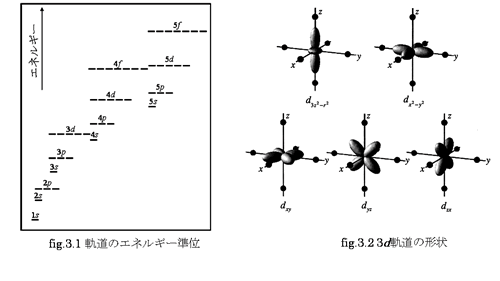
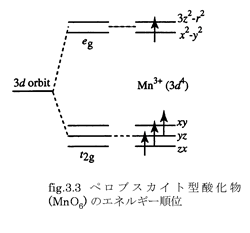軌道自由度を説明するにあたりペロブスカイト型遷移金属酸化物を例として紹介します。ペロブスカイト型遷移金属酸化物では遷移金属イオン(M)を酸素イオン(O)が囲んだ八面体MO₆が一つの結晶の単位となっています。酸素イオンによる結晶場が低対称になってしまうため、磁性を担う3d軌道は酸素を避けるような軌道を持つように三重縮退したt_2g軌道（xy, yz, zx）と酸素方向に軌道を持つように二重縮退したe_g軌道（3z²-y², x²-y²）に分裂し、Hund則にしたがって軌道を埋めていきます(fig.3.3)。Mn³⁺イオンの場合、3d軌道は(t_2g)³(e_g)¹という電子状態を取ることになるので、二重縮退したe_g軌道（3z²-r², x²-y²）のどれかに入るという自由度が生まれます。つまり、縮退した基底状態の下で、電子がどのような軌道をとるかという自由度として定義が可能です。このことを軌道自由度と呼びます。